
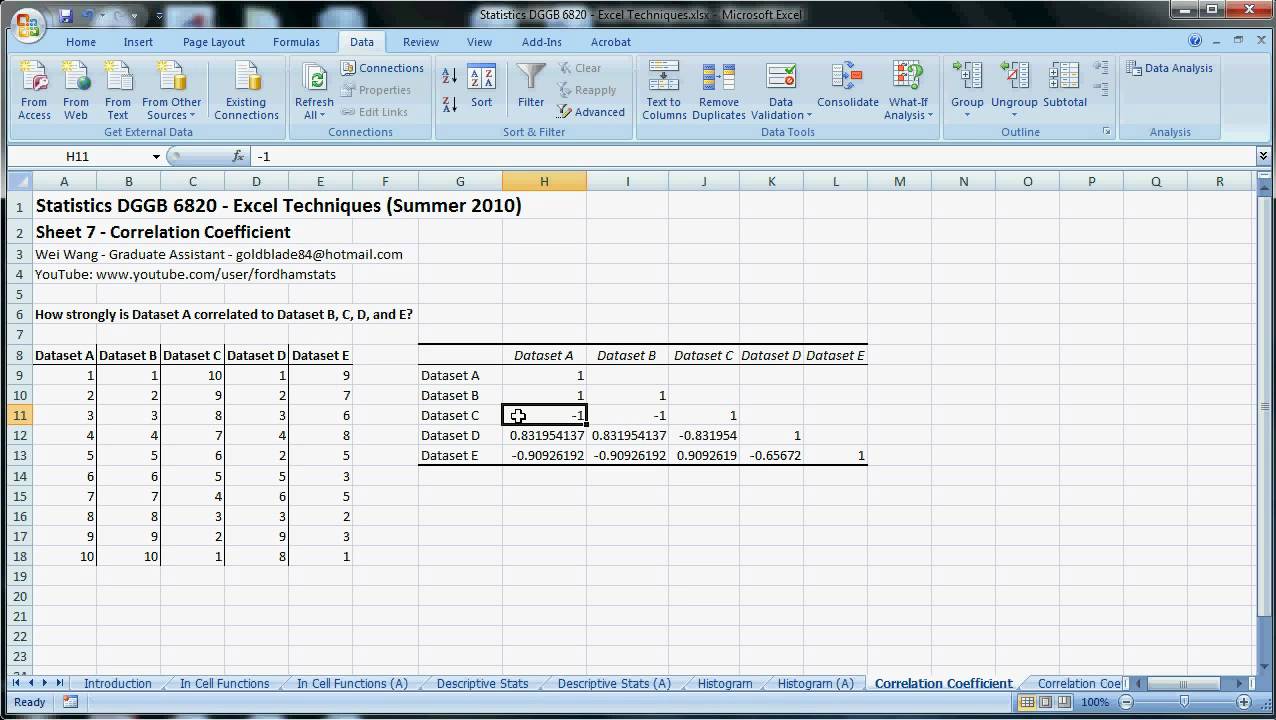
A plot of r k against k is known as a correlogram. The autocorrelation function ( ACF) at lag k, for k ≥ 0, of the time series is defined by The autocovariance function at lag k, for k ≥ 0, of the time series is defined by Note that γ 0 is the variance of the stochastic process.ĭefinition 2: The mean of a time series y 1, …, y n is įor Moran's I, the formula in Y1 is array-entered (press ctrl+shift+Enter instead of just Enter), then copied into Y2:Y10.Definition 1: The autocorrelation function ( ACF) at lag k, denoted ρ k, of a stationary stochastic process, is defined as ρ k = γ k/ γ 0 where γ k = cov(y i, y i+k) for any i.
Those formulas represent Sigma(j=1 to 10) for each x. To simplify, I created helper formulas in columns Y (for Moran's I) and Z (for Geary's C). In Excel, it is difficult (for me) to formulate the double-sigma, a mathematical presentation of nested summations. I just filled the data and weights ranges with random prime numbers.

Honestly, I do not know what values are reasonable for the real purpose of those mathematical formulas (spatial autocorrelation). See the formulas in A3 and A4, and follow their dependencies.įor demonstration purposes, I created data in X1:X10 and "weights" in w!A1:J10, a 10-by-10 matrix. (All cell references are in the "data" worksheet, unless they are qualified with a different worksheet name.)Īlternatively, I also provide an implementation with Excel formulas only. The function calls are demonstrated in A6 and A7 in the "data" worksheet. Alternatively, right-click on a worksheet tab, click on View Code, and double-click on Module1 on the left side of the VBA window. The mathematical formulas are easiest to implement as VBA user-defined functions. Download "moran and geary.xls" ( click here) for reference. I believe I can help you with the Excel implementation. I posted that information for alansidman's benefit and for other potential responders who might want the mathematical definitions.


 0 kommentar(er)
0 kommentar(er)
